搜索 K
Appearance
算法分析
1. 什么是算法分析
当我们说算法分析的时候我们在说什么？（狭义的技术层面的定义）：
算法分析指的是：对算法在运行时间和存储空间这两种资源的利用效率进行研究。 即时间效率和空间效率。
时间效率指算法运行有多快；
空间效率指算法运行时需要多少额外的存储空间。
时间效率也叫时间复杂度；
空间效率也叫空间复杂度。
在计算机时代早期，时间和空间这两种资源都是及其昂贵的。但经过半个多世纪的发展，计算机的速度和存储容量都已经提升了好几个数量级。 现在空间效率已经不是我们关注的重点了，但时间效率的重要性并没有减弱到这种可以忽略的程度。
所以，当我们分析一个算法的的时候，我们重点关注它的时间效率。
2. 算法分析思路
算法分析通用思路： 当我们遇到一个算法时，我们可以用这样一个通用的思路去分析它：
1. 输入规模
首先第一步考虑这个算法的输入规模是什么？
即输入参数，再换句话说也就是待解决的问题有多大？ 从这里入手是因为一个显而易见的规律就是，不管使用什么算法，输入规模越大，运行效率肯定会更长。 比如只对100个数字进行排序，不管你用什么排序算法，时间效率都差不多。只有在输入规模变大的时候，算法的差异才变得既明显又重要了起来。
2. 运行时间的度量单位
接下来第二步考虑这个算法的运行时间，即这个算法运行地快慢。 我们可以简单地用计时的方法，即某个算法运行了多少毫秒。 但这个方式有一个缺陷就是在不同计算机上，相同算法的运行时间是不一样，因为有的电脑快有的电脑慢。
所以有没有一种度量方法可以排除这些无关因素？
答案是肯定的，我们可以关注算法执行了多少步，即操作的运行次数。而且为了简化问题我们只需关注最重要的操作步骤，即所谓的基本操作，因为基本操作已经足够可以决定这个算法的品质。 比如一个算法通常是最内层的循环中是最费时的操作，那我们就只需要把它循环了多少次作为基本操作进行研究。
总而言之就是，对基本操作的大规模输入情况下的变化的研究才更具有深远意义。
4. 算法的最优、最差和平均效率
当我们了解了输入规模对算法时间效率的会产生影响，但算法的执行效率却不仅仅只受输入规模的影响，某些情况下，算法的执行效率更取决于输入参数的细节。
比如：一个简单的顺序查找的算法，在数组里查找数字 9： 在数组 arr1 = [1, 2, 3, 4, 5, 6, 7, 8, 9] 里查找数字 9 和在相同的输入规模的另一个数组 arr2 = [9, 1, 2, 3, 4, 5, 6, 7, 8]里查找数字 9，在数组 arr2 的执行效率肯定更高。
上面小例子中的两个数组就体现了两个极端：输入最优情况和输入最坏情况。 相对应的，
在输入最优情况下的算法就叫最优效率；
在输入最坏情况下的算法就叫最差效率；
在这里有两个经验性的规则：
- 最优效率的分析远远不如最差效率分析重要（因为最差效率可以确定算法运行时间的上界）；
- 如果一个算法的最优效率都不能满足我们的要求，那么我们就可以立即抛弃它。
在现实情况下，输入是“随机”的，既不会是最优输入也不会是最坏输入。所以这里又要引出一个概念，即：平均效率。
首先指出，我们绝不能用“最优效率”和“最差效率”的平均数求得平均效率，即便有时间这个平均数和真正的平均效率巧合地一致。
正确的步骤是：我们要对输入规模 n 做一些假设。 对于上面的顺序查找算法的例子，标准的假设有两个：
- 输入里包含目标数字，那么算法会成功查找到目标数字，此时，成功查找概率是 p(0 <= p <= 1)；
- 对于任意数字 i，匹配发生在数组的第 i 个位置的概率是相同的。
基于这两个假设求平均效率可得：
- 成功查找到目标的情况下，对于任意 i，成功匹配发生在第 i 个位置的概率都是 p/n，此时，算法所做的比较次数是 i；
- 输入数组里不包含目标数字，那么算法不成功查找，比较次数是 n，在这种情况下，可能性是 (1-p)。
由此，平均效率
math
T(n) = [1 * p/n + 2 * p/n + ... + i * p/n + ... + n * p/n] + n*(1-p)
= p/n[1 + 2 + ... + i + ... + n] + n(1-p)
= p/n * n(n+1)/2 + n(1-p)
= p(n+1) / 2 + n(1-p)由此可知，
- 如果 p = 1，也就是说成功率是 100%，查找一定能成功，代入公式可得 (n+1)/2，即大约要查找数组中一半的元素；
- 如果 p = 0，也就是说成功率是 0%，查找必定失败，代入公式可得 n，即算法会对所有元素全部查找一遍。
从这个例子可以发现，平均效率的研究要比最差效率和最优效率的研究困难很多： 我们要将输入规模 n 划分为几种类型，对于同类型的输入，使得算法的执行次数是相同的。
3. 算法时间复杂度的定义
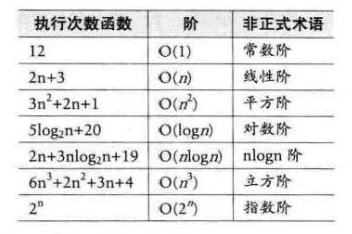
在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度，也就是算法的时间量度， 记作：
math
T(n)= O(f(n))它表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。其中f(n)是问题规模n的某个函数。
用大写O()来体现算法时间复杂度的记法，我们称之为大O记法
常见算法时间复杂度：
- 常数阶O(1)
- 对数阶O(log2n)
- 线性阶O(n)
- 线性对数阶O(nlogn)
- 平方阶O(n^2)，
- 立方阶O(n3)
- k次方阶O(n^k)
- 指数阶O(2^n)
常用的时间复杂度所耗费的时间从小到大依次是:
1. 推导大O阶方法
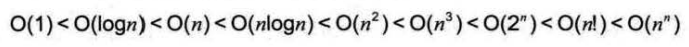
如何分析一个算法的时间复杂度呢？即如何推导大O阶呢？
用常数1取代运行时间中的所有基本操作。
在修改后的运行次数函数中，只保留最高阶项。
如果最高阶项存在且不是1，则去除与这个项相乘的常数。
得到的最后结果就是大O阶。
2. 常见算法的推导
2.1 案例1： 一个数组中寻找最大数 O(n)
java
public class Code_01_FindMax {
public static int findMax(int[] arr) {
int maxNum = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
if (arr[i] > maxNum) {
maxNum = arr[i];
}
}
return maxNum;
}
public static void main(String[] args) {
int[] arr = new int[]{1, 2, 3, 4, 5};
int maxNum = findMax(arr);
System.out.println(maxNum);
}
}2.2 案例2：二分查找O（logn)
java
public class Code_02_BinarySearch {
public static int binarySearch(int[] arr, int key) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
// 为了防止 两数相加会越界
int mid = left + ((right - left) >> 1);
if (arr[mid] < key) {
left = mid + 1;
} else if (arr[mid] > key) {
right = mid - 1;
} else {
return mid;
}
}
return -1;
}
public static void main(String[] args) {
int[] arr = new int[]{1, 4, 7, 9, 10};
int ans = binarySearch(arr, 10);
System.out.println(ans);
}
}2.3 案例3: 两个有序数组中打印相同元素值O（N+M)
java
/**
* 两个有序列表(无重复元素）,寻找相同元素的值并打印
*/
public class Code_03_FindEqualNum {
public static void findEqualNum(int[] arrA, int[] arrB) {
int p1 = 0;
int p2 = 0;
while (p1 < arrA.length && p2 < arrB.length) {
if (arrA[p1] < arrB[p2]) {
p1++;
} else if (arrA[p1] > arrB[p2]) {
p2++;
} else {
System.out.print(arrB[p2] + " ");
p1++;
p2++;
}
}
System.out.println();
}
public static void main(String[] args) {
int[] arrA = new int[]{1, 3, 5, 7, 9};
int[] arrB = new int[]{2, 3, 4, 7, 10};
findEqualNum(arrA, arrB);
}
}4. 额外空间复杂度
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度
案例：数组旋转 O(N)和O（1）两种解法
题目要求：给定一个数组，将数组从第k个位置开始，后面的元素放到数组的前面去，比如将一个数组 [1,2,3,4,5,6,7] 变为 [6,7,1,2,3,4,5]
java
/**
* 数组旋转
*/
public class Code_04_ArrayRotate {
/**
* 实现方法1, 使用临时数组存储，时间复杂度 O(n),空间复杂度 O(n)
* @param arr
* @param idx
*/
public static void arrayRotate1(int[] arr, int idx) {
int[] temp = new int[arr.length];
int j = 0;
for (int i = idx; i < arr.length; i++) {
temp[j++] = arr[i];
}
for (int i = 0; i < idx; i++) {
temp[j++] = arr[i];
}
for (int i = 0; i < arr.length; i++) {
arr[i] = temp[i];
}
}
/**
* 实现方法2：原地反转实现，时间复杂度 O(n),空间复杂度 O(1)
* @param arr
* @param idx
*/
public static void arrayRotate2(int[] arr, int idx) {
reverse(arr, 0, idx - 1);
reverse(arr, idx, arr.length - 1);
reverse(arr, 0, arr.length - 1);
}
/**
* 在指定区间内对数组进行原地反转
* @param arr
* @param start
* @param end
*/
public static void reverse(int[] arr, int start, int end) {
while (start < end) {
swap(arr, start, end);
start++;
end--;
}
}
/**
* 交换数组中指定元素的值
* @param arr
* @param x
* @param y
*/
public static void swap(int[] arr, int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
/**
* 打印数组的公共方法
* @param arr
*/
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = new int[]{1, 2, 3, 4, 5, 6, 7};
arrayRotate2(arr, 5);
printArray(arr);
}
}